Psychological JuJitsu
A college friend of mine introduced me to a game
played with an ordinary deck of playing cards,
that had the very apt name Psychological JuJitsu.
The rules are almost trivial, but the strategy definitely makes one's head
hurt! The object of the game is, in essence, to out-second-guess your
opponent(s). Psychological JuJitsu can be played with 2 or 3 players
(and could no doubt be extended to more, but 2 or 3 is probably best).
The origins of the game are unclear. I've seen posts claiming that it
dates back before World War II, but have not found any actual citations
proving it. One poster reported seeing the Game of Pure Strategy (GOPS)
in "Dave Parlett's Dictionary of Card Games", and that Parlett
dated it to the 1960s. I've also been told that at least one game theory
text also describes the game under this latter name, but again I do not
have an actual citation.
Rules
Separate the deck into suits. Shuffle the diamond suit and place it
face down. Give another suit to each player.
Each card has a value from 1 to 13. Aces are low at 1, jacks
are 11, queens are 12, kings are 13, and other cards have the obvious
values. Players use the cards they start with to bid on the diamonds,
with the object being to collect the greatest total value of diamonds.
There are 13 rounds. Each round, the next card is turned up from the
shuffled diamond suit. Each player then selects one of their "bid"
cards (the suit they were given at the start) and places it face down
in front of them. When everyone has selected a bid, the bids are
revealed, and the highest bid wins the diamond. The cards that were
used to make the bids are then discarded; thus each player will end up
using each of his "bid" cards exactly once in the course of the game.
If the bids are tied in a two-player game, the diamond is discarded.
If there is a tie for high bid in a three-player game the diamond is
placed between the two high bidders and they each get half value for it.
(See variants.) If there is a tie for total value at the end, the game
is a draw.
Psychological JuJitsu is not intended to be a game of memory, so used
bid cards should be left face up in front of the players, making it easy
to see what cards each player still has available. Likewise, the diamonds
that each player has won, and any that are discarded due to ties, should
be kept face up.
Sample Game
Here's a sample two-player game with the players' reasoning shown,
to give you the flavor. Charles is bidding using the clubs;
Scott has the spades.
The first diamond turned up is the 7. Charles is trying a general
strategy of getting diamonds early so he has a lead, forcing Scott to
play catch-up. Scott decides to try a strategy of playing mostly low
cards at first, hoping that Charles will use up lots of high cards.
On the 7, Charles bids 9, and Scott bids 2. (He would have bid 1, but
decided to try 2 just in case Charles was also using an "early low bids"
strategy and chose to bid 1.) Charles wins the 7. The next diamond is
turned up, and the position is as shown below.
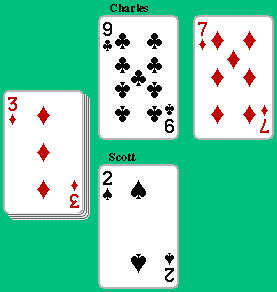 Even Charles, with his "early lead" strategy, has trouble getting too
excited about a 3, so he bids 3. Scott continues with his plan and bids
1. Charles is pleased. (It's always good when you just barely outbid
your opponent, at least in the two-player game.)
Even Charles, with his "early lead" strategy, has trouble getting too
excited about a 3, so he bids 3. Scott continues with his plan and bids
1. Charles is pleased. (It's always good when you just barely outbid
your opponent, at least in the two-player game.)
The next diamond is the 10. Scott decides to risk a "real" bid, hoping that
either Charles will choose to go low this time, or that Charles has noticed
Scott's low-bid strategy and will try to steal the 10 with a medium-sized bid.
Scott tries his 9, but Charles sticks to his plan and bids his queen (12).

Now the diamond king turns up (see position at right). Scott realises he has
to draw the line somewhere, so he bids his king. Charles also bids his
king, and the diamond is discarded. Note that Scott is now guaranteed to
win whatever he chooses to bid his queen on.
Next comes the diamond 2. Charles lets this one go, bidding 1. Scott
likewise bids his smallest remaining card, but in his case that's a 3,
so he gets it.
The next card is the diamond 9. Figuring that Scott will save his
queen to bid on a larger card (the diamond jack or queen), Charles tries
his jack to see if he can grab the 9, or at least get a tie. But Scott
outguesses him and plays his queen now. Not only does he win the 9, but
Scott also continues to have a "sure bid", since now his jack beats all
of Charles's remaining bids.
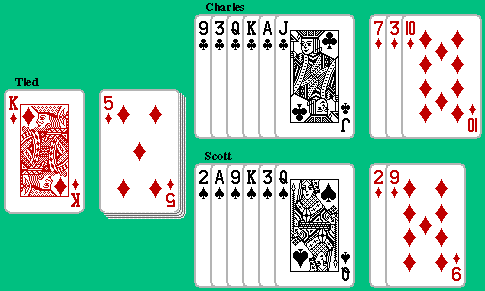
Up comes the diamond 5 (see above). Charles recovers some ground by
bidding 6 against Scott's 4. Scott went low, hoping Charles would bid
higher than that.
On the diamond 8, Charles again gains ground by bidding his lowest card,
the 2, while Scott bids his 10. Scott wins the card but has used up a
powerful bid.
The diamond ace (1) comes up, and each player plays his lowest remaining
card. Scott's 5 beats Charles's 4. The diamond queen is next (see below).

Scott can ensure winning the queen by playing his jack, so Charles is
tempted to play his 5 and preserve what strength he has left. But he
decides it would be disastrous if Scott won the queen using his 8,
keeping the jack in reserve. So Charles plays his 8. (He's not willing
to risk his 10, which would be totally wasted if Scott does play
the jack.) Scott considers his 8, but chooses to play his jack after all.
Scott is now ahead with 32 points of diamonds to Charles's 25. Charles
has a very slight edge in remaining bidding strength: 5 + 7 + 10 compared
to 6 + 7 + 8. The victor is not yet certain, but Charles will need to
do some shrewd guessing in order to win. Basically, (1) he must play his
7 when Scott plays his 6, and (2) he must win the diamond jack. Winning
the diamond jack will require playing his 10, unless Scott plays his 6.
As it happens, the diamond jack comes up next. If Scott plays his 6 and
Charles his 7, Charles will win. (Charles will use his 10 to win the
diamond 6, and Scott will get the diamond 4.) But if Scott does not
play his 6, Charles must play his 10 to have any chance. (Charles still has
to lose one more diamond when he plays his 5, so if he doesn't win the jack
he can't catch up enough.)
After some deliberation, Charles plays his 10, and Scott the 6. Charles
now leads by 4 points, but Scott has a sure victory.
At this point, Charles has the 5 and 7 remaining, and Scott has 7 and 8.
Scott will bid 8 on the diamond 6, and 7 for the diamond 4. He is
guaranteed to win the 6, and Charles cannot do better than tie for the 4.
So Scott picks up 6 points and wins by 2 (see final position below).

Strategy
As was mentioned in the sample game, the bid you usually want to make is
the smallest bid that will beat your opponent's bid. If you could always
play exactly one higher than your opponent, except for playing your ace
when he plays his king, then you will win twelve of the diamonds to his
one. Even if his one is the diamond king, you will blow him away. In
practice, of course, you can't bid that way, but in essence what you are
always trying to do is guess how high your opponent intends to bid, and
then bid just a little bit higher. Conversely, if you think he's
going to bid quite high, you can bid very low, so that his high bid is
"wasted".
In a three-player game, this gets more complex. If both of your opponents
bid about the same, you would like to bid just a little bit higher than
both of them. Again, if they are both bidding quite high, you can do well
by bidding low. If one bids high and the other low, however, you can't
really gain a lot of ground on both of them. You can go high and take the
diamond, or go low and save your strength, but the opponent who played low
will be pacing you. The result you most want to avoid is making a moderate
sized bid and having one opponent bid one higher while the other bids his
lowest card.
In the sample game, one player was able to ensure victory after 11 rounds.
Sometimes that will happen, but other times the game will come down to a
50-50 guess on the next-to-last round. (Obviously, the bids on the last
round are automatic.) Sometimes you may even be able to work out the
complete strategy for the last three rounds. In the sample game, when the
diamond jack came up in round 11, Scott was a 2-to-1 favorite. He could
roll a die and play his 6 one-third of the time, and his 7 the rest of the
time. Charles's best play would be to play his 10 two-thirds of the time,
and his 7 one-third of the time. You can work it through and see that
Charles would win 1/3 of the time and lose 2/3 of the time.
Most of the strategy, however, involves jockeying for position before the
last few cards are played. The sample game illustrated two common
approaches: grab an early lead, and save your big bids for later. Either
of these can work, but the heart of the game lies in adapting your strategy
based on what your opponent is doing (or rather, what you think he's
going to do!). You also have to pay attention to what diamonds are
coming out; the "save your big bids" strategy doesn't do so well if too
many big diamonds come out early.
Smaller Versions
Clearly, under perfect play, each player starts out with the same chance of
winning. Discovering the perfect strategy, however, is quite difficult.
There is no single strategy of the form "bid X for the ace, bid Y for the
two, etc.", that can win, since any such strategy can be beaten by one of
the form "bid X+1 for the ace, Y+1 for the two, etc., and bid 1 when the
other guy bids his king".
Nor is it sufficient for a strategy to involve a random element, where each
bid is randomly determined based on some set of odds. A complete strategy
must also take into account, in determining each bid, what bids the opponent
has already used, and what diamonds have already gone by (and who won them).
There is a different form of the game, in which the players decide up front
how much they are going to bid on each diamond, and cannot change their minds
after seeing how the first few bids go. In this case you don't even really
need the diamonds: the players simply arrange their bids in a face-down pile,
and then start turning up the cards one at a time, and award 1 point to the
high bidder on the first pair, 2 points for the second, etc. Though still
quite complex, this game is much simpler. It also has a lot in common with
a game posted to rec.games.abstract by Colin Bell in 1996, called
Colonel Blotto.
One way to study the complexity of the strategies available is to look at
games played with smaller decks. If each suit has only 3 cards (valued 1,
2, and 3), then the game is trivial: each player bids N for the N of
diamonds. This ensures that the other player cannot do better than draw.
(There are several ways to draw, e.g. bidding 2-3-1 and winning the 1 and 2
of diamonds while losing the 3, but you can't do better.) Once you get to
4-card suits, however, the game is already rather complicated, and the
analysis of the 4-card game leads to some interesting
insights. One point of particular note is that the ability to adjust your
bids based on the results of earlier bidding is key to the game.
When learning the game it's best to play just to see who wins; if you want
to keep score, just count how many games each player wins. Once you've
gotten used to the game, you can start keeping totals of how many points
worth of diamonds you take, and say that the grand total after some number
of hands is the winner.
Another way to score is to award a greater victory if the winner is able to
guarantee victory well in advance. On any round, a player can declare that
he is going to make this bid and all subsequent bids face-up, showing his
bid before the opponent chooses his bid. The score for the game is then
equal to the number of rounds in which that player's bids were face up.
Obviously, the last round's bids can always be made face up, so this means
a game is worth more than 1 point only if someone is willing to start showing
his bids on the 12th round or earlier. (In the sample game, Scott could have
made his last two bids face up, scoring 2.) Note that, if you make a mistake
and realise too late that your face up bids will let the other player win,
you can't stop! You must make all your remaining bids face up, and the
other player will then get the increased score for the game.
A rather nasty variant for the three-player game is to say that, if there
is a two-way tie for the high bid, the other player wins that
diamond. This can lead to rather strange results. In the most extreme
case, two players might bid 13 on the king of diamonds, while the third
player bids 1 and wins it! Though this sort of result is itself probably
not a good feature, the risk of such things happening encourages players to
make their bids less predictable, which can be an improvement.
A variant with two players is to pretend there's a third player who selects
bids at random. Shuffle the remaining suit and, after the actual players
have selected bids, turn up the next card as the dummy player's bid. This
variant detracts somewhat from the psychological element, but can lead to
more complex endgame positions. That is, it may be less likely that one
player will be able to demonstrate a sure victory with several diamonds yet
to bid on.
Another variant (with any number of players) is to have only 12 rounds;
the last diamond does not get bid on and is discarded. Players won't know
until the last round which diamond it is that is being omitted, so someone
who has a "sure winner" bid available (because nobody else has as high a
card left) won't necessarily know when to use it. Note: Since
players will only use 12 bids, they obviously will never use their lowest
bidding card, so you should remove all the aces from the bidding suits.
Perhaps the nastiest variant of all (and one which I only recently thought
of and haven't actually tried) is to add another player who controls the
diamonds. For example, suppose there are four players. Three of them use
the clubs, spades, and hearts to make bids as before. The fourth player
does not bid, but merely chooses what order the diamonds appear in. Each
player pays (say) $1.00 to play the game, and the player with the high score
at the end of the hand takes all the money. The player who controls the
diamonds cannot possibly win the money (except perhaps if there's a three-way
tie bid on every diamond, in which case everyone ends up at zero and
they all split the money). What the diamond player does is make deals with
the other players in which he accepts money in return for his choice of how
to arrange the diamonds.
Initially, of course, all the players are in equivalent positions and there's
no advantage to having one diamond or another turn up. But depending on how
the bids go on the first diamond, there may be a greater expected payoff to
one player depending on which diamond is next. The diamond player would
use this difference in value as a bargaining chip. Also, the diamond player
should start by choosing a diamond that makes it more likely that such an
imbalanced position will be reached.
If you think the preceding variant takes the game to a higher level of
headache, consider the next step. The diamond player's position is clearly
not equivalent to that of the other players. In particular, the other
players could make a deal where they agree to freeze out the diamond
player and whoever wins will split the money (leaving out the diamond
player). Thus the diamond player's contribution to the payout is split
among the other players. So you could imagine letting the diamond player
play for free. But that means that any deal he manages to strike
with any other player is a guaranteed gain for the diamond player, so
perhaps the diamond player should be required to pay some amount,
but how much? Well, how about letting the players bid for the right to
be the diamond player?
Note that this could also be done without the extra player. For instance,
with only two players, each of them could pay $1.00, and then they could
bid to see who gets to control the order of the diamond suit. The winner
then takes the $2.00 plus the diamond-controlling payment.
There are various commercially available games that are clearly
derived from Psychological JuJitsu. Raj introduces negative-valued
cards, for which the low bid wins the undesirable card; Raj is
itself a reprint of the German game Hol's de Geier, which was
released in the late 1980s. The inventor of Hol's de Geier, Alex
Randolph, claims it was based on a game he saw played by Indian members
of the British army in the 1940s; this may explain the pre-WWII reference
mentioned earlier.
High Society, by Reiner Knizia, uses similar equipment but does not
feature simultaneous bidding, which of course makes for a tremendous
difference in play. Players can add to their bids in a continuing
auction, but the amounts they can add are limited to "whole cards" from
their starting set; they cannot "make change" by taking back earlier
portions of their bid. High Society also adds a clever twist at the end:
whoever has the least money left unspent is automatically disqualified;
then whoever has purchased the most points wins.
Pico, a 1996 release from Frank Nestel and Doris Matthaus,
is similar to Psychological JuJitsu but with a much smaller deck.
Players compete with a hand
of five cards drawn randomly from an eleven-card deck; unlike the
other games described above, the cards one plays are also the cards
one hopes to win, rather than a separate deck.
Alan Parr's Dirty Dozen, in addition to having negative and
multiplicative payoff items, has a second deck that determines how the
winner of each item is determined (highest card, lowest card, second
highest, etc.). In each turn, two cards are revealed: a scoring card
and a card indicating how the scoring card will be won.
The title Psychological JuJitsu has also been used for a somewhat
different two-player board game with some similarity of feel. A token
is placed in the middle space of a seven-space track. Each player
begins with a store of 50 points. Each turn, the players simultaneously
reveal a bid of some portion of their remaining points. The higher
bidder moves the token one space towards the opponent. Both players
lose the points bid, and the next turn begins. The first player to move
the token to the far end of the board wins. Knizia's game Tor is
very similar to this, but the bidding units are cards from 1-13, with the
special feature that a 13 loses to any card ranked 1-10.
My thanks to Kevin J. Maroney for much of the above information about
commercial and historical versions.
 Even Charles, with his "early lead" strategy, has trouble getting too
excited about a 3, so he bids 3. Scott continues with his plan and bids
1. Charles is pleased. (It's always good when you just barely outbid
your opponent, at least in the two-player game.)
Even Charles, with his "early lead" strategy, has trouble getting too
excited about a 3, so he bids 3. Scott continues with his plan and bids
1. Charles is pleased. (It's always good when you just barely outbid
your opponent, at least in the two-player game.)



